Rapid prototyping of models for COVID-19 outbreak detection in workplaces | BMC Infectious Diseases

October 23, 2023 steven

We present our two models and results in the sequence they were developed, starting with the exponential model, which we use to explore the effects of growth rate ($R_{\text {eff}}$), test sensitivity and test frequency on the probability of detecting outbreaks in workplaces. We then consider the Agent Based Model (ABM), using it to probe the results of the exponential model and also to explore the impact of more complex work schedules on the probability of outbreak detection.

When these models were developed, Australia had very few cases of COVID-19 and decision-makers were concerned with outbreaks stemming from single positive cases. As such, our modelling is framed around how quickly any case could be detected in “high-risk” workplaces. In particular, we calculate the probability an outbreak is detected within a week. This timeframe was chosen in collaboration with decision-makers.

For both the exponential model and the ABM, we define an outbreak occurring when at least one individual is infected. An outbreak is detected when a positive case is identified, either through testing or symptom onset.

Exponential model

Our initial model for the probability of detecting a COVID-19 outbreak in a workplace assumes exponential growth of active cases. In the exponential model, disease prevalence on day $i+1$ (denoted $P_{i+1}$) is given by:

$$\begin{aligned} P_{i+1} = P_i(R_{\text {eff}})^{\frac{1}{g}}, \end{aligned}$$

(1)

where $P_i$ is the disease prevalence on day i, g is the generation interval and $R_{\text {eff}}$ is the effective reproduction number. We assume a generation interval of 4.7 days, and that an outbreak begins on the first day with one active infection ($P_0 = 1$)[13]. With these assumptions, we calculate the expected number of active cases through time under different values of $R_{\text {eff}}$. We assume all infections are due to contacts within the workplace, that is there are no cases imported into the workplace other than the initially seeded infection. Note that this model does not distinguish between symptomatic and asymptomatic infection. Further details about the exponential model are provided in the Supplementary material.

Using our model of prevalence, we then calculate the probability of detecting at least one case within a week under different testing strategies. We vary testing strategies by considering different test sensitivities and test frequency, i.e. the number of days per week testing occurs. In our results we consider scenarios where testing occurs once per week, three times per week and daily. We assume that on days when testing occurs, the entire workforce is tested. This testing framework was chosen to suit workplaces with high importation risk, such as quarantine hotels.

The one-week detection probability is defined as the probability an infected individual returns a positive test within a week of the initial infection. Let $P_i$ be the prevalence on testing day i, and s the test sensitivity. In our model, we make the simplifying assumption that each test is independent and test sensitivity a) does not vary between people and b) does not varying across a person’s infectious period. Furthermore, we assume tests have $100\%$ specificity. The probability an outbreak is not detected on day i (given everyone is tested) is:

$$\begin{aligned} Pr(\text {no detection on day { i}})&= Pr(\text {all infected people test negative})\end{aligned}$$

(2)

$$\begin{aligned}&= (1-s)^{P_i}. \end{aligned}$$

(3)

Let T be the set of testing days in a given week, i.e. days where everyone is tested. The probability of detection in a week is therefore given by:

$$\begin{aligned} Pr(\text {detection in a week})&= 1- Pr(\text {no detection on all testing days})\end{aligned}$$

(4)

$$\begin{aligned}&= 1 – \prod _{i \in T} Pr(\text {no detection on day} i)\end{aligned}$$

(5)

$$\begin{aligned}&= 1 – \prod _{i \in T} (1-s)^{P_i}. \end{aligned}$$

(6)

Exponential model results

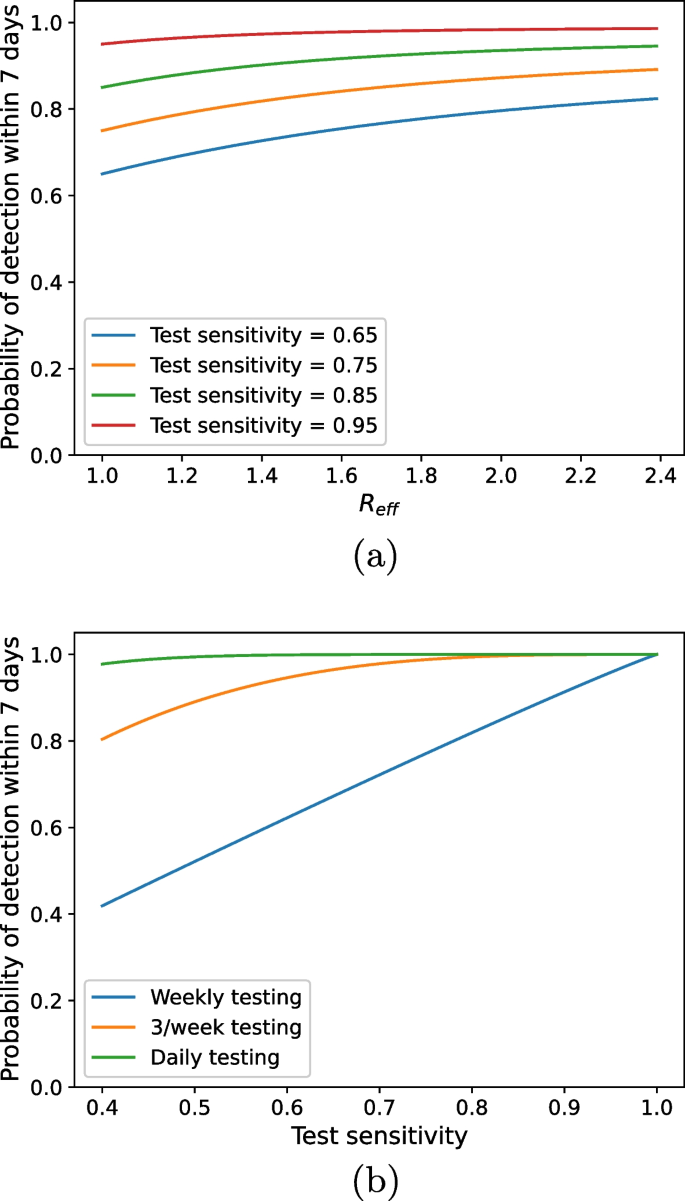
The probability of detection within a week increases with both test sensitivity and $R_{\text {eff}}$ (Fig. 1a). With testing occurring once per week, there is a large difference between whether there is low (0.65) or high (0.95) test sensitivity. However, the difference in the probability of outbreak detection between low and high sensitivity decreases with increasing $R_{\text {eff}}$. As $R_{\text {eff}}$ increases the outbreak spreads faster, meaning more infected people are tested within a week, increasing the likelihood that at least one is detected.

Increasing test sensitivity and frequency both increase the probability of outbreak detection within a week (Fig. 1b). Most notably, daily testing results in a high probability of detection within a week ($>95\%$), for all test sensitivities. This demonstrates that low-sensitivity tests, such as RATs, are still useful for outbreak detection — their shortcomings can be overcome by more frequent testing.

Agent based model

We develop an agent based model (ABM) to represent additional complexities of the workplace setting not captured in the exponential model. The ABM incorporates further complexity and allows us to ask more detailed questions about workplace testing. We start by setting up the ABM using the same set of assumptions as the exponential model. In replicating the exponential model results using the ABM, we can be confident that the ABM generalises the earlier results.

Each agent in our model follows an susceptible–exposed–infectious–recovered disease progression. Agents begin each simulation susceptible, and once infected become exposed. An exposed agent is neither infectious nor detectable. Exposed agents will transition to an incubating phase, where they become both infectious and detectable by testing. In the incubating phase, agents are either symptomatic or asymptomatic. There are no differences in transmission or infection period between symptomatic or asymptomatic individuals, but it allows us to track symptom onset. Both symptomatic and asymptomatic infections are detectable by testing, but symptomatic infection is also detected at the moment of symptom onset. When their infection ends, agents become recovered, and immune to reinfection. Further modelling details, including parameter values, can be found in the Supplementary material.

For each simulation, outbreaks are seeded by a single infection in the workplace. That is, one randomly selected agent starts “exposed” for each simulation. As for the exponential model, there are no infections imported into the workplace other than the initially seeded infection. An outbreak is detected at symptom onset of an infected person or when a positive test result is returned. As for the exponential model, we assume test sensitivity is constant across all people and across infectious periods, and that the tests have 100% specificity. We assume that two thirds of infectious people are symptomatic. For each model simulation, we estimate the probability of detecting at least one case within a week over 5000 simulation instances, each of which is subject to stochastic variation. We calculate this probability as the proportion of simulation instances resulting in outbreak detection within a week.

When considering the ABM under the exponential model assumptions, we assume there is no latency period and no detection via symptom onset. As there is no difference in transmission or infection period between symptomatic and asymptomatic infections, we can simulate the ABM with no detection via symptom onset by considering all infections to be asymptomatic. This is simply for ease of calculation and does not imply in this case we only consider asymptomatic testing.

We define test frequency by specifying the number of testing days per week. As in the exponential model, on days when testing occurs, everyone attending the workplace is tested.

To extend the exponential model results, we consider the effects of intermittent work schedules on outbreak detection. We define these work schedules by specifying the proportion of the workplace working 1, 3, 5 or 7 days a week. Employees are then randomly assigned work days in accordance with the number of days they are scheduled to work. We assume people are only tested at work, but outbreaks may be detected through symptom onset at any time, regardless of whether the unwell individual is present in the workplace.

Agent based model results

In this section, we present results from the ABM. We start by reproducing results from the exponential model to see how the ABM aligns with previous results. We then update our assumptions to consider the impact of intermittent workplace attendance on the probability of outbreak detection within a week of the introduction of the virus.

Comparing the exponential and agent based models

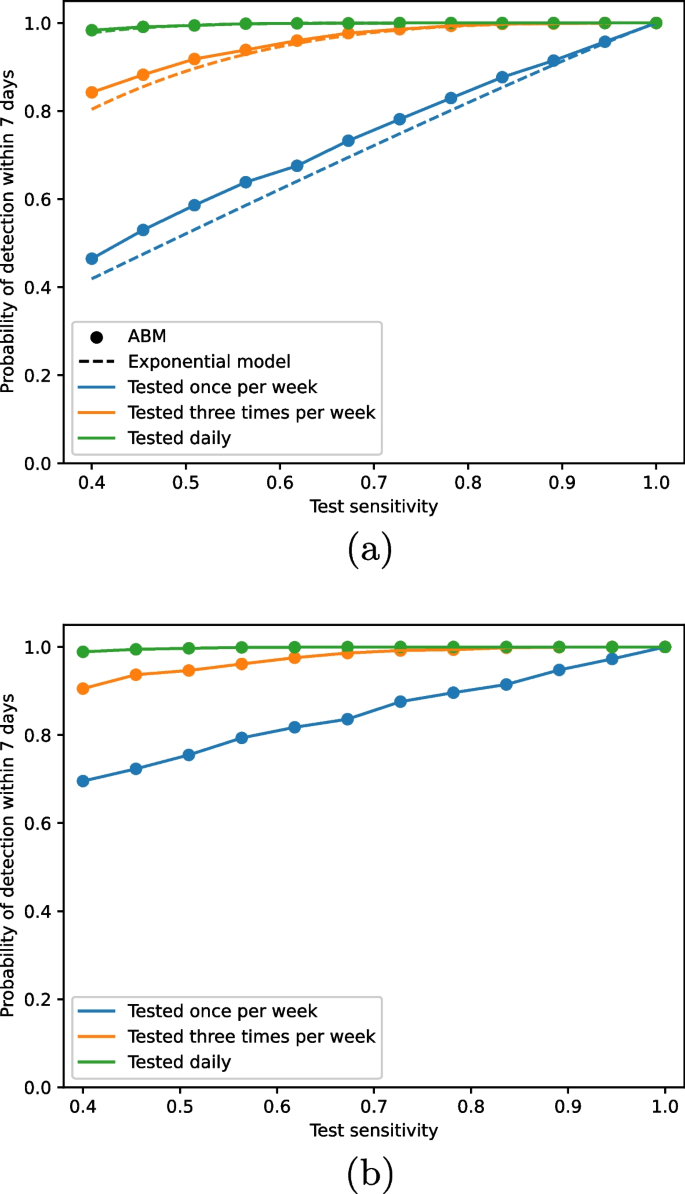
In line with the process of rapid prototyping, Fig. 2 compares the exponential model behaviour to that of the ABM. Under identical sets of assumptions, the ABM results closely follow those of the exponential model (Fig. 2a), although the ABM produces slightly more optimistic estimates of detection probability. However, when we change assumptions of the ABM (Fig. 2b), the results begin to diverge. Under the new assumptions, the results from the ABM produce much higher probabilities of outbreak detection than the exponential model. This is explained by the additional mode of detection, by symptom onset. The additional assumptions we use here cannot be built into the exponential model due to its simplicity, so the development of the ABM allows us to explore the impact of these infection and testing characteristics on outbreak detection.

Intermittent workplace attendance

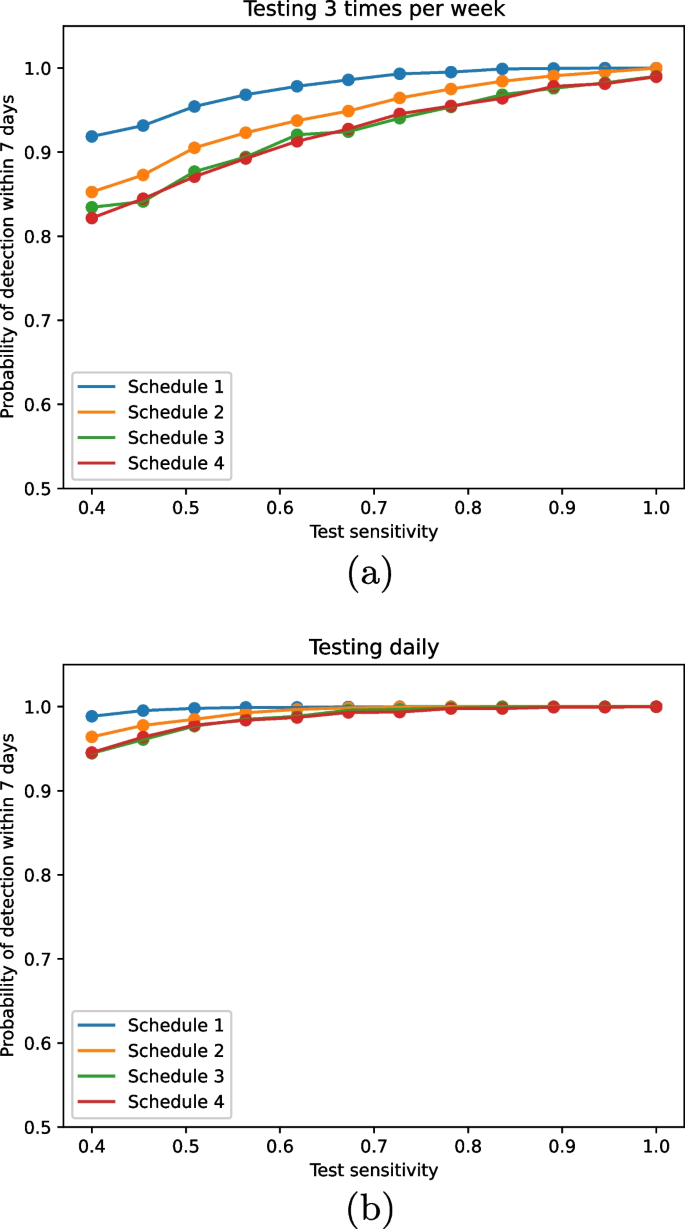
A strength of the ABM is that it can be used to explore the implications of more complex patterns of workplace attendance. We introduce an intermittent work schedule, where some proportion of workers work 1, 3, 5 and 7 days a week. Analogously to the testing assumptions of the exponential model, we assume that when testing occurs, everyone in the workplace on that day is tested. We consider the following intermittent work schedules defined by the proportion of the workforce working 1, 3, 5 or 7 days a week:

1

$100\%$ 7 days/week,
2

$100\%$ 5 days/week,
3

$60\%$ 5 days/week, $40\%$ 3 days/week,
4

$60\%$ 5 days/week, $30\%$ 3 days/week, $10\%$ 1 day/week.

As observed in the exponential model, increasing test frequency and sensitivity increases the probability of detecting an outbreak (Fig. 3). In a similar way, the detection probability is higher when employees work more frequently. Notably, even for a sparse work schedule, low test sensitivity can be compensated for with higher testing frequency. If we increase test frequency, employees are more likely to be tested in a given week as they are more likely to be at work on a testing day. This compounds the benefits of frequent testing observed in the exponential model.

The ABM includes the assumption that outbreaks can be detected by symptom onset, which imposes an upper bound on the time to detection. As symptom onset can occur outside the workplace, outbreaks can be detected even when an infected worker is at home. This bound increases the seven-day detection probability compared to the exponential model.

Source link